| |
This is the necessary condition. Now we need to concentrate on the sufficient condition prove.
Assume the 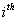 state is transient, i.e., state is transient, i.e., 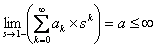 . Using the two stated facts given below : . Using the two stated facts given below :
| (i) |
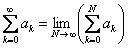 if converges then if converges then 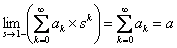 |
and
| (ii) |
 for for 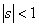 |
we can infer 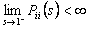 .Again utilizing the fact that if .Again utilizing the fact that if 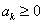 and and  , then , then 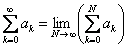 which leads us to which leads us to 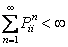 being true. On seeing this we can immediately conclude that it contradicts our hypothesis based on which we started, i.e., being true. On seeing this we can immediately conclude that it contradicts our hypothesis based on which we started, i.e., 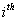 state is transient. Hence state is transient. Hence 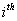 state is not transient. state is not transient.
|