| |
Corollary based on Theorem 1.3
Is the following holds true, i.e., 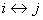 , and if , and if 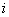 is recurrent, then is recurrent, then 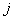 is also recurrent. is also recurrent.
Proof of corollary based on Theorem 1.3
If 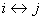 , then there exists , then there exists 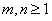 , such that we have , such that we have 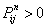 and and 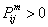 . Now if . Now if 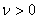 , which is arbitrary, we can obtain , which is arbitrary, we can obtain 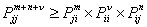 , which we utilize to sum up, which leads us to , which we utilize to sum up, which leads us to 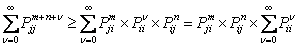 . Now if . Now if 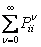 diverges, so does diverges, so does 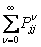 . Now we already know that a state . Now we already know that a state 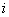 is recurrent iff is recurrent iff 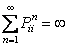 , hence it would immediately lead us to the fact that , hence it would immediately lead us to the fact that 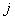 is recurrent if is recurrent if 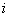 is recurrent. is recurrent.
|