| |
Theorem 1.3
A state 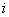 is recurrent iff is recurrent iff 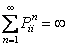
Proof of Theorem 1.3
Assume state 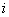 is recurrent then we must have must have is recurrent then we must have must have 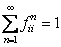 , which is what we need to prove. Now pay close attention to the concept of generating function from where we see that, , which is what we need to prove. Now pay close attention to the concept of generating function from where we see that, 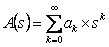 , , 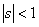 and this is the generic form,from which we have (i) and this is the generic form,from which we have (i) 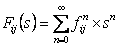 , , 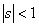 , i.e., (ii) , i.e., (ii) 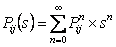 , , 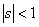 (proof given above),would also imply (proof given above),would also imply 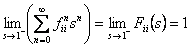 , which would immediately prove that , which would immediately prove that 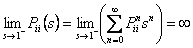 , as , as 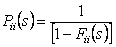 for for 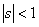 (refer above prove). Now using the second proof which is: if (refer above prove). Now using the second proof which is: if 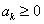 and and 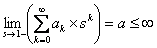 , ,
|