Assignment 1.1
A psychological subject can make one of the two responses marked by 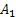 and and 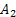 , and associated with each response are a set of , and associated with each response are a set of  stimuli, i.e., stimuli, i.e., 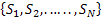 . Each stimulus is conditioned to one of the responses. A single stimulus is sampled at random and all possibilities are equally likely and the subject responds according to the stimulus sampled. Reinforcement occurs at each trial with probability, . Each stimulus is conditioned to one of the responses. A single stimulus is sampled at random and all possibilities are equally likely and the subject responds according to the stimulus sampled. Reinforcement occurs at each trial with probability, 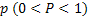 independence of the previous history of the process. When reinforcement occurs, the stimulus sampled does not alter its conditioning state. In the contrary event the stimulus becomes conditioned to the other response. Consider the Markov chain whose state variable is the number of stimuli conditioned to responseA1 . Determine the transition probability matrix for this Markov chain. independence of the previous history of the process. When reinforcement occurs, the stimulus sampled does not alter its conditioning state. In the contrary event the stimulus becomes conditioned to the other response. Consider the Markov chain whose state variable is the number of stimuli conditioned to responseA1 . Determine the transition probability matrix for this Markov chain.
Solution of Assignment 1.1
Let 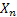 denote the number of stimuli conditioned to the response A1 at the nth trial. Clearly, denote the number of stimuli conditioned to the response A1 at the nth trial. Clearly, 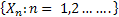 represent the Markov chain with discrete state space represent the Markov chain with discrete state space 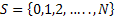 and the transition probabilities for this Markov chain are as followes. and the transition probabilities for this Markov chain are as followes.
and
and
Hence the transition probability for this Markov chain is given as shown below:

|