| |
For the recurrent state, the mean recurrence time value is given by 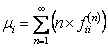 , and if , and if 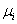 is infinite then the state is infinite then the state 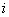 is null recurrent, and in case is null recurrent, and in case 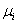 is finite then the state is finite then the state 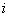 is positive recurrent. We must remember that is positive recurrent. We must remember that 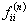 , , 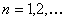 are the corresponding probabilities that state are the corresponding probabilities that state 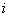 is revisited after the first, second, third, etc., transition times. In a similar line, is revisited after the first, second, third, etc., transition times. In a similar line, 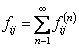 , i.e., the sum of the probabilities that the state after starting from the , i.e., the sum of the probabilities that the state after starting from the 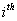 state goes to state goes to 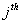 state after state after 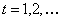 time. So as time. So as 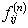 is the first passage probability, hence mean of the first passage time is given by is the first passage probability, hence mean of the first passage time is given by 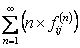 . .
Suppose a Markov chain starts at the 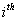 state and comes back to the state and comes back to the 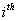 state again, but only after time periods of state again, but only after time periods of 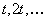 and and 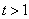 , then state , then state 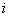 is periodic, with a periodicity of is periodic, with a periodicity of 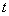 (where this (where this 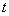 is the largest integer with this property). This would imply that is the largest integer with this property). This would imply that 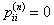 apart from when apart from when 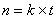 , , 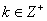 . A state which is not periodic is called aperiodic. Just note that for a aperiodic state the periodicity is 1. An aperiodic state which is positive recurrent is called ergodic state. Below for our own convenience we summarize the definitions for a Markov chain . A state which is not periodic is called aperiodic. Just note that for a aperiodic state the periodicity is 1. An aperiodic state which is positive recurrent is called ergodic state. Below for our own convenience we summarize the definitions for a Markov chain
|