| |
Few definitions which are useful are
Ephemeral state : A state 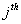 is called ephemeral state if is called ephemeral state if 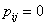 , , 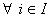 , i.e., this state cannot be reached from any other state. Now if we think rationally, the Markov chain can only be in the ephemeral state initially (because the process has not yet started) and pass out of the ephemeral state after the first transition, i.e., after , i.e., this state cannot be reached from any other state. Now if we think rationally, the Markov chain can only be in the ephemeral state initially (because the process has not yet started) and pass out of the ephemeral state after the first transition, i.e., after 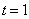 . Now if the characteristics of the ephemeral state are to be understood from the transition probability matrix point of view, then we have the ephemeral state as denoted by that state for which in the transition probability matrix all the probability values corresponding to that state (denoted by the corresponding column) are zeros as shown in the matrix P. . Now if the characteristics of the ephemeral state are to be understood from the transition probability matrix point of view, then we have the ephemeral state as denoted by that state for which in the transition probability matrix all the probability values corresponding to that state (denoted by the corresponding column) are zeros as shown in the matrix P.
 |
Let us suppose that the Markov chain is initially at state 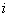 , also let , also let 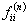 be the probability that the next occurrence of state be the probability that the next occurrence of state 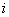 is at time is at time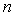 , i.e., , i.e., 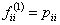 and for and for 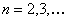 , we have , we have 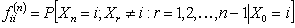 , which implies that the probability that based on the condition that the Markov chain started at , which implies that the probability that based on the condition that the Markov chain started at 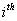 state at time state at time 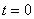 , and would again be at , and would again be at 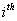 state at time state at time 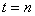 , provided it did not ever come to the , provided it did not ever come to the 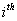 state at any of the times state at any of the times 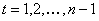 . This . This 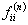 is the first return probability for time is the first return probability for time 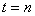 . Similarly first passage probability, . Similarly first passage probability, 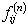 , as the conditional probability that state , as the conditional probability that state 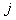 is avoided at times, is avoided at times, 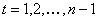 , and entered at time , and entered at time 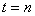 , given that , given that 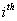 state is occupied initially. Thus we should have state is occupied initially. Thus we should have 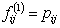 and for and for 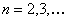 , we have , we have 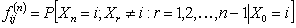 , ,
|