| |
Now refer to the statement that recurrence and periodicity are class property, which means that all states in an equivalence class are either recurrent or non-recurrent. So for one dimension and two dimension all the states in that class are recurrent, but in three dimension it means that once the particle leaves the origin, it never returns to that state.
Few classifications of the states and their corresponding limit theorems
The states of a Markov chain can be classified into distinct types depending on their respective limiting behavior. Suppose the Markov chain's initial state is 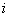 and its final state is and its final state is 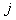 . So if the ultimate return of the Markov chain to this . So if the ultimate return of the Markov chain to this 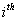 is a certain event then that state, is a certain event then that state, 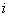 , is called a recurrent state and the time of return for the first time, which is obviously a random variable is called the recurrent time. In case the mean recurrence time for the first time return to the , is called a recurrent state and the time of return for the first time, which is obviously a random variable is called the recurrent time. In case the mean recurrence time for the first time return to the 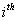 state, provided the Markov chain started from the state, provided the Markov chain started from the 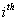 state, is finite, then the state is called positive recurrent, else if it is infinite then the state is non-recurrent. Also we already know that in case the ultimate return to the state, is finite, then the state is called positive recurrent, else if it is infinite then the state is non-recurrent. Also we already know that in case the ultimate return to the 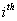 state has a probability of less than one, then the state is called transient. state has a probability of less than one, then the state is called transient.
|