| |
(i) 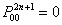 , , 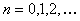
(ii)  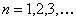
Thus we have
The above result can be obtained if we note that 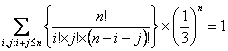 . Now this fact that . Now this fact that 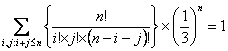 is true for this case as is true for this case as 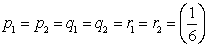 , else we have to rework the whole problem. , else we have to rework the whole problem.
Again going back to 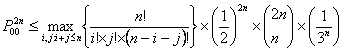 , we see that for , we see that for 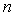 being a large value we have being a large value we have 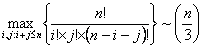 when when 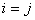 , i.e., , i.e., 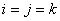 . Thus we have . Thus we have
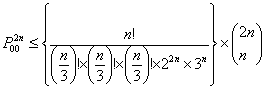 , and again using Stirling's formula or approximation, which is , and again using Stirling's formula or approximation, which is 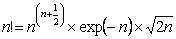 , we have the right hand side as , we have the right hand side as 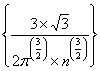 , when , when 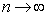 . But if we have to find . But if we have to find 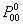 , , 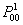 , …., then the sum, i.e., , …., then the sum, i.e., 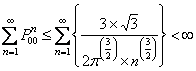 , which is the property of transient state and not recurrent state. , which is the property of transient state and not recurrent state. |