Consider again the simple case where a molecule (in a n adiabatic enclosure is randomly fluctuating all around the chamber or box, such that it rebounds from the walls and all other molecules without any loss of total energy. Consider the chamber has infinite dimension, such that there are infinite number of such states for the molecule. This problem of stating that the molecules have infinite states to visit is not impractical, as we can consider the chamber of finite size, but considering the size of the molecule it can take visit pr occue at infinite states. We can prove this formulae (which we will find out soon) for the case when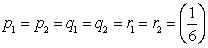