| |
Assignment 1.2
(a) Suppose 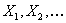 are independent with the following probabilities, i.e., are independent with the following probabilities, i.e., 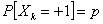 and and 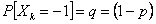 , and , and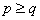 .With .With 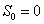 , set , set  , , 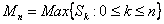 and and 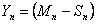 . If . If 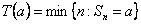 , then show that , then show that
.
(b) Now if we consider the bivariate process 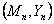 as a random walk on the positive two dimension lattice, then what is the probability that this random walk leaves the rectangle at the top? as a random walk on the positive two dimension lattice, then what is the probability that this random walk leaves the rectangle at the top?
|