Examples 1.13
Let 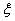 be discrete random variables such that the realized values of be discrete random variables such that the realized values of 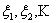 , are non-negative integer values, such that , are non-negative integer values, such that 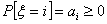 and and 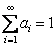 We must remember that the observations are independent. From this We must remember that the observations are independent. From this 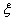 we define two Markov processes which are. we define two Markov processes which are.
Case 1: Consider 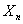 , , 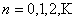 such that such that 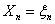 and assume (which is not at all difficult to do so considering that is the initial conditions for any process which is known beforehand) and assume (which is not at all difficult to do so considering that is the initial conditions for any process which is known beforehand) 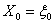 , then the Markov matrix is given by , then the Markov matrix is given by 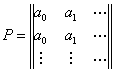 , where the fact that each row is exactly equal due to the simple fact that the random variable , where the fact that each row is exactly equal due to the simple fact that the random variable 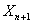 is independent of is independent of 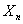
Case 2: Another class of important Markov chains is seen when we consider the successive partial sums, 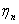 of of 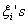 , , 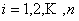 , i.e., , i.e., 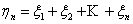 . By definition we have . By definition we have 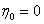 . Then the process . Then the process 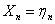 is a Markov chain and we can easily calculate the transition probability matrix as is a Markov chain and we can easily calculate the transition probability matrix as
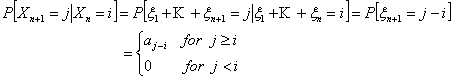
Here we use the independence of 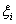
Thus writing the transition probability matrix we have it of the following form, which is

If the possible values of the random variables are permitted to be both positive as well as negative integers, then instead of labeling the states by non-negative integers, as we usually do, we may denote them with the totality of the state space, which will make the transition matrix look more symmetric in nature, such that we denote it like
 , ,
where 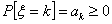 , , 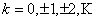 and and 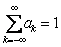
|