| |
Examples 1.14
Consider a one dimensional random walks, whose state space is a finite or infinite subset 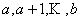 of integers, such that a particle at state of integers, such that a particle at state 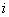 can in a single transition move to can in a single transition move to 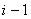 or or 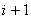 state or it can remain at the same state, state or it can remain at the same state, 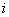 . Now all these three movements has some probability such that we . Now all these three movements has some probability such that we 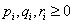 , , 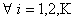 , and , and 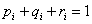 . It is also true that . It is also true that 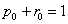 . So that we have (i) . So that we have (i) 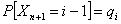 , (ii) , (ii) 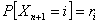 and and 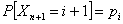 . It is obvious that . It is obvious that 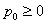 , , 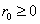 and and 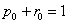 , hence given these set of information one can write the transition matrix as below , hence given these set of information one can write the transition matrix as below

Let us consider a gamble as an example of simple random walk. Suppose that we have two persons, say Ram and Shyam with initial amounts of A and B INR with them respectively. Consider the probability of Ram winning one unit from Shyam is 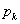 and the corresponding of losing one unit is and the corresponding of losing one unit is 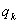 , where , where 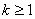 and and 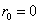 . So in case if we denote . So in case if we denote 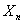 the fortune of Ram after n such change in position, then the fortune of Ram after n such change in position, then 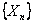 clearly denotes a random walk. It is very easy to see that once the state reaches either 0 or clearly denotes a random walk. It is very easy to see that once the state reaches either 0 or 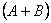 , the process remains in that state. This process is known as the gambler's ruin, and in that case the transition probability matrix is given as shown below , the process remains in that state. This process is known as the gambler's ruin, and in that case the transition probability matrix is given as shown below
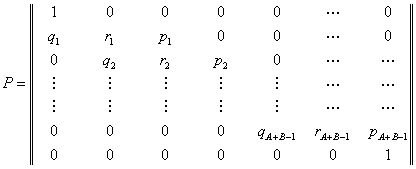
Different variants of this game can be constructed so that we have different examples of random walk, some of which are briefly discussed below in order to motivate the reader in the application aspect of random walks.
|