Wald's Equations
Consider 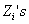 be the sum of random numbers random variables (r.v's), i.e., be the sum of random numbers random variables (r.v's), i.e., 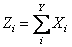 and remember that and remember that 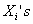 are i.i.d random variables (r.v's), then are i.i.d random variables (r.v's), then 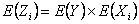 . The basic concepts of Wald are the founding stones based on which the rich branch of Sequential Analysis (Sequential Estimation, Sequential Interval Estimation and Sequential Hypotheses) have developed. . The basic concepts of Wald are the founding stones based on which the rich branch of Sequential Analysis (Sequential Estimation, Sequential Interval Estimation and Sequential Hypotheses) have developed.
Now if we have 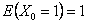 , then , then 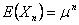 . Without repetition we would like to mention that for the interested readers we would advice that rather than panic they should wait till we cover the simple proof of Wald's equations. Remember the importance of this equation stems from the fact that one can also find variance which is given by . Without repetition we would like to mention that for the interested readers we would advice that rather than panic they should wait till we cover the simple proof of Wald's equations. Remember the importance of this equation stems from the fact that one can also find variance which is given by 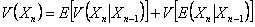 . .
Stationary transition probability
When the one state transition probabilities are independent of time, i.e., 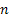 , we say we have a Markov process which has stationary transition probabilities. , we say we have a Markov process which has stationary transition probabilities.
Thus if 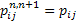 , then we all know the transition probability matrix is denoted as , then we all know the transition probability matrix is denoted as 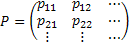 , i.e., , i.e., 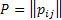 and this is the Markov matrix or the transition probability matrix of the process. So generally the and this is the Markov matrix or the transition probability matrix of the process. So generally the 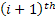 row of row of 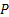 denotes the distribution or the collection of realized values of denotes the distribution or the collection of realized values of 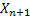 under the condition that under the condition that 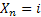 . If the number of states are finite then the transition probability matrix, . If the number of states are finite then the transition probability matrix, 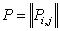 , is a square matrix. Also it would be true that we have , is a square matrix. Also it would be true that we have
(i) 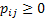 , , 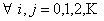
(ii) 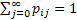 , , 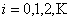
Now the whole process, i.e., 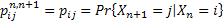 is known if we know the value of is known if we know the value of 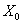 , or more generally the probability distribution of the process. , or more generally the probability distribution of the process.
Assume 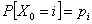 , given which we want to calculate , given which we want to calculate 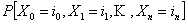 which is any probability involving which is any probability involving 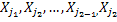 ,such that using the axioms of probability. ,such that using the axioms of probability.
Thus
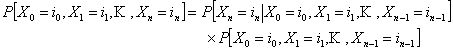 |
(1.1) |
By definition of Markov process we also have
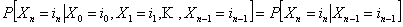 |
(1.2) |
Substituting (1.2) in (1.1) we have
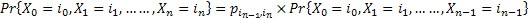
Further more in the next step we have
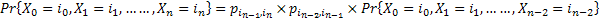
Using induction we finally have
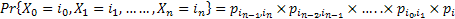
To make things better for understanding and also to bring into light the usefulness
of Markov chains we give few more examples which we are sure would be appreciated by the readers. |