Let us pictorially illustrate the concept in Figure 1.21, where we start at 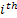 state at time state at time 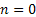 and after and after 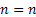 time it come back to time it come back to 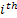 state. If one observes closely the main difference with Figure 1.18 is the fact that here we denote the states while in Figure 1.18 it was the time which was depicted along the line. state. If one observes closely the main difference with Figure 1.18 is the fact that here we denote the states while in Figure 1.18 it was the time which was depicted along the line.
The colour scheme in Figure 1.21 is quite easy to understand if we concentrate on the fact that it can be green line starting at 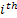 position at position at 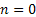 and returning to and returning to 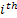 position at position at 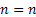 for the first time. While the blue would denote that reaches for the first time. While the blue would denote that reaches 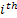 position once at position once at 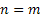 time and then again the stochastic process continues till it reaches time and then again the stochastic process continues till it reaches 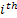 position at position at 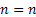 for the second time. Continuing with the same logic we can have such visits to for the second time. Continuing with the same logic we can have such visits to 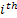 position many number of times but remembering that position many number of times but remembering that 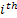 position is reached at position is reached at 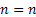 , i.e., , i.e., 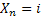 . .
Then we have
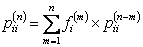 , from which it is easy to note that , from which it is easy to note that
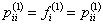 for for 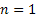
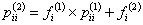 for for 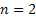 . .
Utilizing this two formulae we easily get
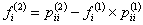
Furthermore through simple induction we can show that
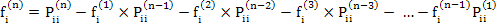
So the probability that the systems ever returns to its original state 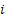 is given is given 
Hence
- fi = 1 Þ that the system returns to state
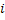 in a certain number of steps in a certain number of steps
- fi = 0 Þ that the system never returns to state
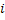
- fi < 1 Þ that the system may or may not returns to state i in a certain number of steps
One can understand that these transitional probabilities are dependent on (i) initial and final states and (ii) time of transition from the initial to the final states, i.e., 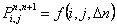 , where , where 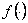 is of some function form of is of some function form of 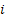 , , 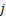 as well as difference in time periods. as well as difference in time periods.
|