Recurrence
Consider an arbitrary state, 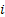 , which is fixed, such that for all integers, , which is fixed, such that for all integers, 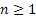 , we define: , we define: 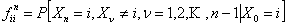 , which is basically the probability that after having started from the , which is basically the probability that after having started from the 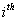 state it comes back to state it comes back to 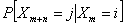 state for the first time ONLY at the state for the first time ONLY at the 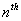 transition. The definition makes it clear that transition. The definition makes it clear that 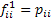 and and 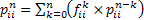 for for 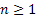 , and we also define , and we also define 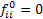 Now let us consider the simple illustrations (Figure 1.19 and Figure 1.20). Now let us consider the simple illustrations (Figure 1.19 and Figure 1.20).
From both the figures (Figure 1.19 and Figure 1.20) it is clear that 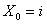 and and 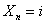 and the first return to state and the first return to state 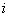 occurs at occurs at 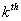 transition. If this return is denoted by event transition. If this return is denoted by event 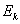 , then the events , then the events 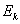 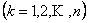 are mutually exclusive. are mutually exclusive.
Now the probability of the event that the first return is at the 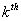 transition is transition is 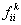 which we already know. Now for the remaining which we already know. Now for the remaining 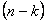 transitions we will only deal with those such that transitions we will only deal with those such that 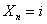 holds true. In case it does not, we will not consider that. holds true. In case it does not, we will not consider that.
So we have
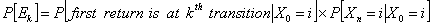
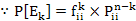 for for 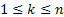 and we also have and we also have 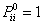
Hence
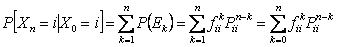 as as 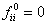
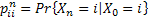
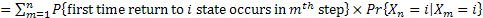 |