| |
Classification of the states of a Markov Chain
In this classification we will mention state j as being accessible from another state i, i.e., 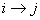 if if 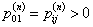 for some for some 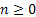 , here , here 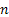 denotes the denotes the 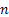 stage transition. In case if it not, then the state j is not accessible from state i. stage transition. In case if it not, then the state j is not accessible from state i.
Example 1.12
Let us consider a conditional probability matrix as given below
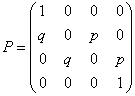 . .
Few observations from Example 1.12
- Then if the question is asked, is state 3 accessible from state 1, the answer is No.
- No state can be reached from state 1, i.e., state 1 is like a sink as
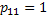 and it is called the absorbing state. Similarly once you reach state 4 you remain in that state for ever as and it is called the absorbing state. Similarly once you reach state 4 you remain in that state for ever as 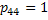 and it is also called the absorbing state. and it is also called the absorbing state.
- Similarly
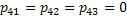 . .
- It is possible to go from state 3 to state 1, i.e., 3 to 2 to 1, but reverse is not possible.
- In case we have
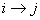 as well as as well as 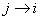 , then the two states are communicating between themselves. So in the example given above we have , then the two states are communicating between themselves. So in the example given above we have
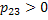 as 2 leads to 3 and also as 2 leads to 3 and also 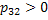 as 3 leads to 2, hence state 2 and state 3 are communicating states. as 3 leads to 2, hence state 2 and state 3 are communicating states.- A set of states in a Markov chain is said to be closed if pij = 0 for i Î C and j Ï C, what ever the set C be.
- If a subset of a Markov chain is closed then the subset also forms a Markov chain
- If a Markov chain has no closed subset, i.e., if the Markov chain is itself not closed, then the Markov chain is said to be irreducible.
- Further more if
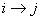 and and 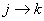 , it implies that , it implies that 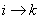 , which means we are only required to show that , which means we are only required to show that 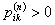 for some for some 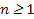 . .
Note
Now suppose we know that 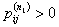 and and 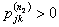 and since and since 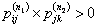 , then from Chapman Kolmorogrov equations we can show that , then from Chapman Kolmorogrov equations we can show that 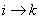 , is true, i.e., , is true, i.e., 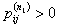 as as 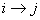 and and 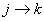 are both true and this statement that are both true and this statement that 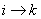 is true will hold for some n ³ 1. For the interested readers we would advice that rather than panic they should wait till we cover the simple proof of Chapman Kolmorogrov equations. is true will hold for some n ³ 1. For the interested readers we would advice that rather than panic they should wait till we cover the simple proof of Chapman Kolmorogrov equations.
Consider a fixed, but arbitrary state 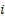 and suppose at time and suppose at time 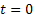 it is at state it is at state 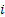 , i.e., X0 = i, and also define , i.e., X0 = i, and also define 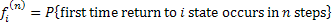 , i.e., at the , i.e., at the 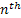 step I am back at state i. step I am back at state i.
|