| |
So generalizing we can write
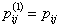 , , 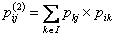 , , 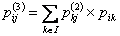 and so on. and so on.
Figure 1.18 thus shows how the stochastic process starts at 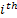 state at time state at time 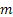 and finally goes to and finally goes to 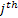 state at time state at time 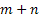 . What is interesting to note it how does this transition takes place. A general understanding of the stochastic process movement would make it clear that the process could have arbitrarily been at . What is interesting to note it how does this transition takes place. A general understanding of the stochastic process movement would make it clear that the process could have arbitrarily been at 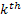 state at say any point of time state at say any point of time 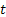 between between 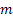 and and 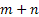 , i.e., , i.e., 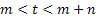 , and the colour scheme of red, blue and green should make this arbitrary movement clear. , and the colour scheme of red, blue and green should make this arbitrary movement clear.
Using matrix notation we already have 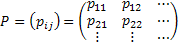 , such that , such that 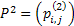 , where it means the element in the , where it means the element in the 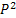 matrix and not that we simply multiply pij X pij. Thus it means that matrix and not that we simply multiply pij X pij. Thus it means that 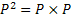 . Similarly we have . Similarly we have 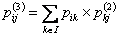 , hence , hence 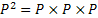 .Thus generalizing we have .Thus generalizing we have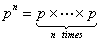 and also and also 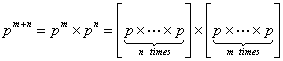 .Here it must be remember that we are considering there is no structural breaks or change in the underlying distribution i.e., .Here it must be remember that we are considering there is no structural breaks or change in the underlying distribution i.e., 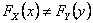 . If that occurs then some where we would have the transition probability matrix general structures as different, i.e., for t = m, m+1,…, m* we have . If that occurs then some where we would have the transition probability matrix general structures as different, i.e., for t = m, m+1,…, m* we have 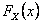 as the underlying distribution, and afterwards from t = m*+1, m*+2,…, m*+n the distribution is as the underlying distribution, and afterwards from t = m*+1, m*+2,…, m*+n the distribution is 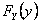
Hence the basic thing required is to know the one step transition matrix is pij.
If 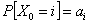 and and 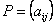 are given then are given then 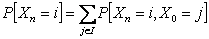 , i.e., , i.e.,
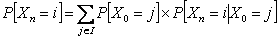 , i.e., , i.e.,
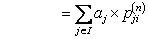 , ,
Thus we have the probability in terms of intermittent probability and the transition matrix |