| |
Few relevant information which is important
Consider Bi are mutually exclusive and exhaustive events, such that 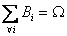 , which is the sure event, i.e., technically the whole of the sample space and also assume , which is the sure event, i.e., technically the whole of the sample space and also assume 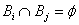 , , 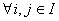 is true. Now suppose is true. Now suppose 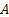 and and 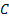 are events, such that we write are events, such that we write 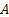 as as 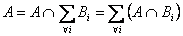 . Then what may be of interest to us is to find . Then what may be of interest to us is to find 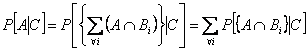
Now due to the fact that 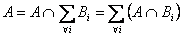 is true, we can write the following, i.e., is true, we can write the following, i.e., 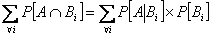 , so with conditional probability , so with conditional probability 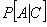 now becomes now becomes
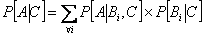
Pictorially we can denote this as following as shown in Figure 1.17.
|
Figure 1.17: Illustration of the concept of conditional probability and joint distribution |
Hence we can write
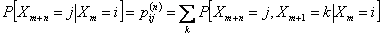 as |
|
|
|
Hence: 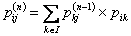 . . |