Before we proceed with some proves relevant for our stochastic processes we need to see and understand two important proves, which are stated as Lemmas (Lemma 1.1 (a) and Lemma 1.1 (b)) below.
Lemma 1.1 (a)
If 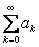 converges (i.e., converges (i.e., 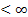 ) then it implies (i.e., ) then it implies (i.e., 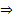 ) ) 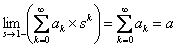
Proof of Lemma 1.1 (a)
What we will prove here is 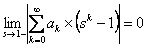 (see carefully this is what we have to prove as written above) (see carefully this is what we have to prove as written above)
Since 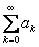 converges then for any converges then for any 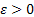 one can find one can find 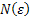 such that such that 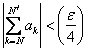 holds true for all values of holds true for all values of 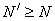 , then choose that N and write , then choose that N and write
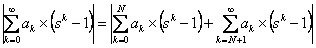
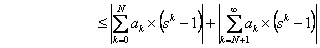
Now for 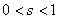 we have we have
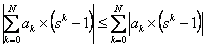
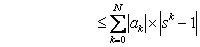
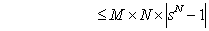 , where , where 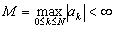
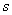 being sufficiently close to 1 we have being sufficiently close to 1 we have
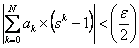 [this can be arbitrarily done considering any combination of [this can be arbitrarily done considering any combination of 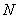 and and 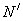 , such that , such that 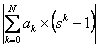 can be made lesser and lesser to can be made lesser and lesser to 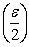 ]. ].
Now we need to find the second term which is 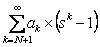 , hence we have , hence we have
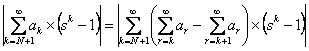
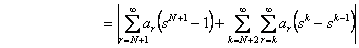
Look carefully and we immediately note that the first term is bounded by 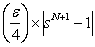 , while the second term is bounded by , while the second term is bounded by 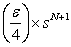 . Hence we have . Hence we have 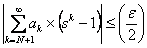
Combining these two we have 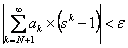 , provided , provided 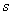 being sufficiently close to 1. being sufficiently close to 1.
|