Module 1:Concepts of Random walks, Markov Chains, Markov Processes
Lecture 2:Random Walks
Lemma 1.1 (b)
(b) If and , then
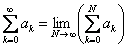
Proof of Lemma 1.1 (b)
Since for , hence the case of is obvious. In case , then by our hypothesis for , hence for . Now as is a monotone increasing function in , hence it has a finite limit which will be equal to . Here remember we utilize the result proved from (a).
and 
, then 
for 
, hence the case of 
is obvious. In case 
for 
, hence 
for 
. Now as 
is a monotone increasing function in 
, hence it has a finite limit which will be equal to 
. Here remember we utilize the result proved from (a).
