| |
Theorem 1.2
1) If 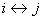 , then , then 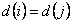
2) If any state 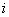 has the value of periodicity as has the value of periodicity as 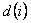 , then there exists an integer N (depending on , then there exists an integer N (depending on 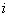 ), such that for all integers ), such that for all integers 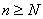 , , 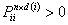
3) If 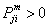 , then , then 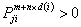 for all n (positive integer) sufficiently large for all n (positive integer) sufficiently large
A Markov chain for which each state has periodicity of one (1) is called aperiodic.
Generating functions
Let us first define the concept of general generating function. In case we have a sequence, 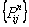 , then the generating function, , then the generating function, 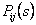 , is defined as , is defined as 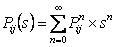 for the case when for the case when 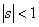 . Hence in a similar manner the generating function for the sequence . Hence in a similar manner the generating function for the sequence 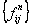 , , 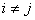 , is given by , is given by 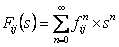 , , 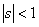
We know that if we have (i) 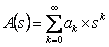 , , 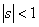 and (ii) and (ii) 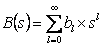 , , 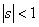 , then we can write the product of , then we can write the product of 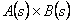 as given below, i.e., as given below, i.e.,
Let us identify 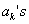 with the with the 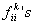 and the and the 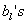 with the with the 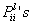 and if we compare and if we compare 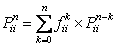 for for 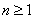 with with 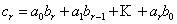 we immediately obtain we immediately obtain 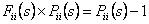 for for 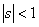 or or 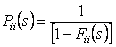 for for 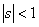
One should remember that 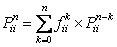 for for 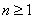 is not valid for n = 0 and using simple arguments we have is not valid for n = 0 and using simple arguments we have
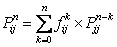 for for 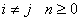
where 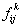 is the probability that the first passage from state is the probability that the first passage from state 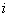 to state to state 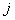 occurs at the occurs at the 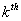 transition. Again transition. Again 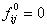 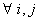 , and utilizing , and utilizing 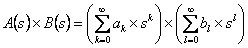 , we can easily show that , we can easily show that 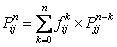 for for 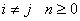 can be written as can be written as 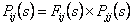 , , 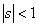
We say a state 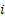 is recurrent iff is recurrent iff 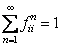 , i.e., a state is recurrent iff the probability is 1 so that starting at state , i.e., a state is recurrent iff the probability is 1 so that starting at state 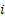 it will return to state it will return to state 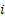 after a finite number of transitions. A non-recurrent state is said to be transient. after a finite number of transitions. A non-recurrent state is said to be transient.
|