| |
Transition probability matrices of a Markov chain
A Markov is completely defined by one step transition matrix and the specifications of a probability distribution on the state of the process at time t=0. Given this, what is of main concern is to calculate the n-step transition probability matrix, i.e., 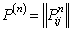 , where , where 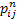 is the probability that the process goes from state is the probability that the process goes from state 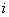 to state to state 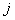 in in 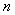 transitions, thus we have transitions, thus we have  and remember this is a stationary transition probability. and remember this is a stationary transition probability.
Theorem 1.1
If one step probability matrix of a Markov chain is 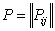 , then , then 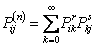 for any fixed pair of nonnegative integers for any fixed pair of nonnegative integers 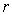 and and 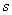 , satisfying , satisfying 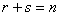 , where we define , where we define
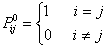
Proof of Theorem 1.1
The proof is very simple. Consider the case when, 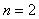 , i.e., the event when we move from state , i.e., the event when we move from state 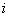 to to 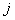 in two transitions in mutually exclusive ways such that the first transition takes place from in two transitions in mutually exclusive ways such that the first transition takes place from 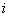 to to 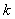 state and then from state and then from 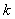 to to 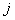 state. Here state. Here 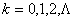 . Now because of Markovian assumption the probability of first transition from state . Now because of Markovian assumption the probability of first transition from state 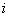 to state to state 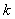 is is 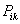 , and that of moving from state , and that of moving from state 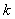 to to 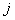 is is 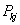 . If the probability of the process initially being at state . If the probability of the process initially being at state 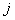 is is 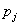 , then the probability of the process being at state , then the probability of the process being at state 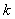 at time at time 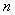 is given by is given by 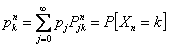 . What is of main interest to us is to find . What is of main interest to us is to find 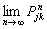 , and for doing that we need to describe few important properties of Markov chain, which we now again do in order to have a better understanding of this process. , and for doing that we need to describe few important properties of Markov chain, which we now again do in order to have a better understanding of this process.
Properties
|