Examples 1.16
Let us consider the example given below
|
0 |
1 |
2 |
3 |
4 |
5 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
½ |
0 |
½ |
0 |
0 |
0 |
2 |
0 |
½ |
0 |
½ |
0 |
0 |
3 |
0 |
0 |
½ |
0 |
½ |
0 |
4 |
0 |
0 |
0 |
½ |
0 |
½ |
5 |
0 |
0 |
0 |
0 |
0 |
1 |
From the matrix above we can easily find out the equivalence classes as: 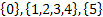 . .
Examples 1.17
In case the matrix is of the following form as shown below:
|
0 |
1 |
2 |
3 |
4 |
5 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
½ |
0 |
½ |
0 |
0 |
0 |
2 |
0 |
½ |
0 |
½ |
0 |
0 |
3 |
0 |
0 |
½ |
0 |
½ |
0 |
4 |
0 |
0 |
0 |
½ |
0 |
½ |
5 |
0 |
0 |
0 |
0 |
1 |
0 |
Then the equivalence class is only one and it is 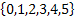
Equivalence class and Irreducible Markov chain
Let us now partition the totality of the states into equivalence classes, such that the states in equivalence class are those that communicate with each other. A Markov chain is irreducible if the equivalence property or relation induces only one class, i.e., all states communicate. Thus in irreducible Markov chain all the states communicate with each other. For the example given below,
i.e.,

We have three equivalence classes, which are 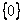 , , 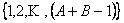 , , 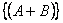 , such that , such that
1) 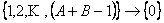 true true
2) 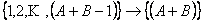 true true
3) 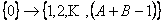 false false
4) 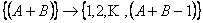 false false
5) 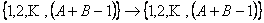 true true
|