| |
As this particle is subjected to random collision and impulses, which happens due to the particle being bombarded by all other gas particles, as well as the wall of the container, hence its position changes randomly, though the particle as such can be described by its continuous path of movement. With the important assumption that the future position of the particle, i.e., say B depends only on its present position, say A, then the process denoted by 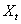 is such that is such that  is Markovian, and is Markovian, and 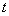 here is the time. A discrete approximation of this continuous process is provided by the random walk, and a classical discrete version of the Brownian motion is provided by the symmetric random walk. A symmetric random walk is a Markovian chain where the state space is the continuous real line (we consider a simple example here on), and the transition probability is given as below, i.e., here is the time. A discrete approximation of this continuous process is provided by the random walk, and a classical discrete version of the Brownian motion is provided by the symmetric random walk. A symmetric random walk is a Markovian chain where the state space is the continuous real line (we consider a simple example here on), and the transition probability is given as below, i.e.,
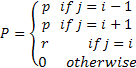 , ,  where where 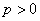 , , 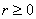 , , 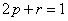 , and for the symmetric random walk we have , and for the symmetric random walk we have 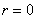 , , 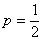
What is important to note about the stochastic process is the initial condition, based on which we can find all the characteristics of the process. Now consider the transition probability matrix given as
 ,such that in case ,such that in case
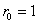 , and , and 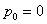 , then state 0 is the absorbing state, such that once the process reaches state 0 it continues staying there. Now when , then state 0 is the absorbing state, such that once the process reaches state 0 it continues staying there. Now when 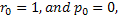 then state 0 acts as a reflecting state, like a molecule rebounding after hitting the wall (Figure 1.22). then state 0 acts as a reflecting state, like a molecule rebounding after hitting the wall (Figure 1.22).
Figure 1.22: A gas molecule moving randomly inside the chamber but rebounding from the walls
|