| |
Examples 1.15
The significance of random walks is not only apparent in different examples of gambling, but also is also evident (due to the reasonable and good discrete approximations) to many physical process which are to do with diffusion of particles, or particles which are continuously colliding and being randomly bombarded, say for example gas particles in a gas chamber which we can for theoretical situation considering as adiabatic (i.e., no heat is being transferred into or out of the system) process, such that when a particle collides with another particle or with the wall of the container it rebounds with the same level of total energy. Thus as the particles are subjected to collisions and random impulses then its (any single particle) position fluctuates randomly but it does describe a continuous path. For simplicity if we consider the future position to be dependent on the present position, then the process denoted by 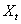 is such that is such that  is Markovian, where is Markovian, where 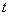 is the time. A discrete approximation to such a continuous motion corresponds to a random walk. A classical example is the symmetric random walk, where the state space is denoted is the totality of all integers and if the general transition probability matrix values or elements is given by is the time. A discrete approximation to such a continuous motion corresponds to a random walk. A classical example is the symmetric random walk, where the state space is denoted is the totality of all integers and if the general transition probability matrix values or elements is given by 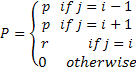 , , 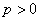 where where 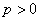 , , 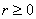 , , 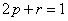 , and for the symmetric random walk we , and for the symmetric random walk we
have 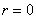 , , 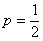
Now the question which is apparent is the fact that why are random walks so useful? Apart from the above examples which are all related to gambling, can we find some interesting examples of random walks? The answer is yes. Apart from gambling (which by itself is very interesting and exciting), random walks are frequently used as approximations to describe a variety of physical process, e.g., diffusion of particles. Let us give an example where we consider a gas particle in a box as shown in Figure 1.21, whose initial position is A (xA, yA, zA) which are given by the Cartesian coordinate system X, Y and Z. Now consider after some time the gas particle is at position B (xB, yB, zB).
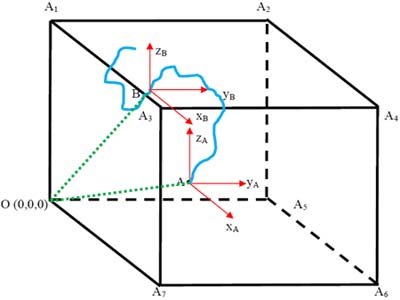
Figure 1.21: A gas molecule moving randomly inside the chamber
|