| |
Sequential sampling methodologies
One is aware that as 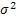 is unknown, is unknown, 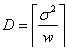 is also unknown. Hence using fixed sampling rule will not help us to solve our problem of finding the minimum sample size. This implies, one has to take the recourse of some multistage or adaptive sampling techniques to solve this problem. We discuss few of the multistage or adaptive sampling methodologies used in literature to circumvent such bounded risk estimation problem. is also unknown. Hence using fixed sampling rule will not help us to solve our problem of finding the minimum sample size. This implies, one has to take the recourse of some multistage or adaptive sampling techniques to solve this problem. We discuss few of the multistage or adaptive sampling methodologies used in literature to circumvent such bounded risk estimation problem.
Two-stage sampling procedure: Consider a two-stage sampling procedure, where at the first stage a sample of size 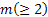 is drawn to estimate the unknown quantity is drawn to estimate the unknown quantity 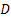 which is calculated using which is calculated using 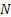 . Here . Here 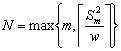 , is the estimate of the number of observations, needed to satisfy the bound placed by , is the estimate of the number of observations, needed to satisfy the bound placed by 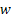 . The methodology works as follows. Start with X1, X2,….., Xm observations in a single batch and determine N. If N = m, then we stop and do not take any more observations in the second stage. However if N > m, then one samples an additional (N - m) observations in the second stage. Based on the total observations X1, X2,….., XN, the estimator, . The methodology works as follows. Start with X1, X2,….., Xm observations in a single batch and determine N. If N = m, then we stop and do not take any more observations in the second stage. However if N > m, then one samples an additional (N - m) observations in the second stage. Based on the total observations X1, X2,….., XN, the estimator, 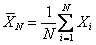 is calculated. We must remember since is calculated. We must remember since
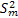 is the result of a random procedure, is the result of a random procedure, 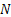 , the sample size is also a random number. , the sample size is also a random number.
Purely sequential sampling procedure: Next consider a purely sequential methodology, which starts with a sample of size 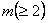 and one continues to take one observation at a time until, and one continues to take one observation at a time until,  , where , where 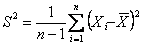 is the best estimate of is the best estimate of 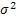 which is recalculated each time the sample size, n, changes. In other words, the estimator is updated at each stage with the arrival of each new observation, until the stopping rule is met for the very first time. Once sampling stops the value of m is evaluated using its estimator which is recalculated each time the sample size, n, changes. In other words, the estimator is updated at each stage with the arrival of each new observation, until the stopping rule is met for the very first time. Once sampling stops the value of m is evaluated using its estimator 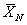 . Thus it establishes the superiority of the purely sequential sampling procedure over the two-stage procedure from a statistical asymptotic viewpoint and not from the practical perspective. . Thus it establishes the superiority of the purely sequential sampling procedure over the two-stage procedure from a statistical asymptotic viewpoint and not from the practical perspective.
Three-stage sampling procedure: Even though from the theoretical standpoint, purely sequential sampling procedure satisfies the asymptotic second-order efficiency property, yet one immediately realizes that taking one observation at a time, as is done in the purely sequential sampling scheme, is practically inconvenient. Hence in order to save sampling operations and at the same time maintain the second-order property, different authors have considered the three-stage sampling procedure. This methodology is as follows. Let 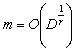 , for some r > 1. That is, the starting sample size m is allowed to grow, but in a manner that , for some r > 1. That is, the starting sample size m is allowed to grow, but in a manner that 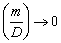 as as
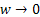 , which implies that m is allowed to increase at a slower rate than , which implies that m is allowed to increase at a slower rate than 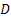 as as 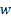 becomes smaller. After having fixed becomes smaller. After having fixed
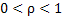 and with the starting sample size of and with the starting sample size of 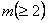 , let , let
Here T estimates 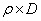 , which is a fraction of D. If T = m, then we do not sample any more in the second stage, but if T > m, one samples the difference (T - m) in one single batch. Based on the observations {X1, X2, ….., XT} one now proceeds to find N which is the estimator of , which is a fraction of D. If T = m, then we do not sample any more in the second stage, but if T > m, one samples the difference (T - m) in one single batch. Based on the observations {X1, X2, ….., XT} one now proceeds to find N which is the estimator of 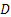 . If now N = T, then we do not take any more sample in the third stage, but if N > T, the difference (N - T) of observations are taken in the third stage to find the value of N. After the sampling procedure terminates,the estimator . If now N = T, then we do not take any more sample in the third stage, but if N > T, the difference (N - T) of observations are taken in the third stage to find the value of N. After the sampling procedure terminates,the estimator 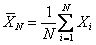 determines the estimated value of determines the estimated value of
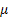 (the location parameter for the normal distribution). One must remember that even if there is a huge amount of variability in the last (N - T) observations, still we are certain to terminate our sampling procedure following the same stopping criteria. If the variability in the last (N - T) observations is appreciable, then the number of observations one needs to take in the third, i.e., the last stage would be quite high. It is observed that such a three-stage procedure apart from obeying the asymptotic consistency and asymptotic first order efficiency properties, also obeys the asymptotic second order efficiency property. (the location parameter for the normal distribution). One must remember that even if there is a huge amount of variability in the last (N - T) observations, still we are certain to terminate our sampling procedure following the same stopping criteria. If the variability in the last (N - T) observations is appreciable, then the number of observations one needs to take in the third, i.e., the last stage would be quite high. It is observed that such a three-stage procedure apart from obeying the asymptotic consistency and asymptotic first order efficiency properties, also obeys the asymptotic second order efficiency property.
|