| |
Application of renewal theory and renewal theory concepts
Example 5.1
A very simple example and illustration for renewal theory which has wide application is in sampling, and the area is known as sequential sampling. So first let us illustrate the concept of sequential sampling methodology or also called multi-stage sampling techniques.
Before that, let us illustrate the concept of bounded risk and its implications with a simple example. This concept of bounded risk will facilitate our understanding of sequential sampling methodology in a much better way. Furthermore we will illustrate through detailed examples four different distributions using two different loss functions, which we are sure will help the reader appreciate the application of renewal theory through its use in sequential sampling procedure.
Consider a normal distribution with the probability distribution function (p.d.f.) given by 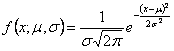 , ,
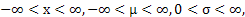 with both mean with both mean
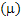 and variance and variance
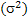 unknown. Suppose one is interested to find the point estimate of m (location parameter) subject to a squared error loss (SEL) function, given by L(Tn,q) = (Tn-q)2. After recording X1, X2,….., Xn observations, we find the sample mean unknown. Suppose one is interested to find the point estimate of m (location parameter) subject to a squared error loss (SEL) function, given by L(Tn,q) = (Tn-q)2. After recording X1, X2,….., Xn observations, we find the sample mean 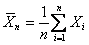 , which is the estimator of m. The corresponding associated risk is given by , which is the estimator of m. The corresponding associated risk is given by 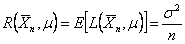 . Next suppose we require this risk to be such that it does not exceed a pre-assigned known value, w (> 0). We immediately see that if . Next suppose we require this risk to be such that it does not exceed a pre-assigned known value, w (> 0). We immediately see that if 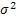 (square of scale parameter) is known then the optimal sample size, (square of scale parameter) is known then the optimal sample size, 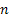 , is , is 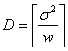 . But with . But with 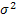 unknown the problem cannot be solved with any fixed sampling techniques and hence we can take recourse to the use of sequential sampling procedures which are briefly discussed below. unknown the problem cannot be solved with any fixed sampling techniques and hence we can take recourse to the use of sequential sampling procedures which are briefly discussed below. |