| |
Accelerated sequential sampling procedure: Another variation of the purely sequential sampling methodology cuts down on the cost by accelerating the original sequential procedure. Here also one starts with a sample size of 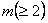 and after having fixed and after having fixed 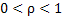 and with and with 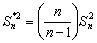 define define

Thus one first samples purely sequentially obtaining X1, X2,.…., XR such that R estimates 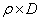 and then proceeds to estimate D by N. If T = R, then we do not take any more samples, but if T > R, then one samples (T - R) observations in one single batch thus curtailing sampling operations and comes up with the estimate of the location parameter and then proceeds to estimate D by N. If T = R, then we do not take any more samples, but if T > R, then one samples (T - R) observations in one single batch thus curtailing sampling operations and comes up with the estimate of the location parameter 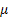 . The asymptotic second-order properties of such accelerated sequential procedures have also been developed by different authors. . The asymptotic second-order properties of such accelerated sequential procedures have also been developed by different authors.
Batch sequential sampling procedure: In batch sequential sequential sampling procedure, we first consider
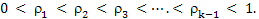 . We also specify . We also specify 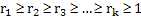 and ti's, where ri (i = 1, 2, ….., k) denotes the minimum number of observations one takes at each and every step in the ith batch, while ti, is the number of such steps one is required to take in that ith batch. The connotation of minimum number of observations means the number of observations or individuals one takes at one go. Thus if we have k number of batches, then for the ith (i = 1, 2, ….., k) batch, the number of observations one would take is and ti's, where ri (i = 1, 2, ….., k) denotes the minimum number of observations one takes at each and every step in the ith batch, while ti, is the number of such steps one is required to take in that ith batch. The connotation of minimum number of observations means the number of observations or individuals one takes at one go. Thus if we have k number of batches, then for the ith (i = 1, 2, ….., k) batch, the number of observations one would take is 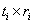 , and for the whole batch sequential sampling procedure it is , and for the whole batch sequential sampling procedure it is 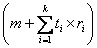 , where , where 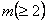 is the number of observations required to initiate the batch sequential sampling procedure. Remember, this is the number of observations required to initiate the batch sequential sampling procedure. Remember, this 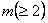 number of observations is taken at one go in the first step which is literally the zero batch. One should also remember that r1, r2, r3,….., rk and number of observations is taken at one go in the first step which is literally the zero batch. One should also remember that r1, r2, r3,….., rk and 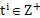 . . The procedure works as follows. Start with a sample size of . . The procedure works as follows. Start with a sample size of 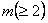 and for each batch follow the sampling methodology according to the rule give below and for each batch follow the sampling methodology according to the rule give below
 |