| |
Note
- Since the inter arrival times are i.i.d, hence at each renewal or event the process probability starts over again.
- There are finite numbers of renewals which can occur in a finite time, as by the strong law of large numbers (SLLN) we can show that
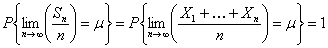 . But since . But since 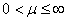 , hence , hence 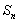 must go towards infinity as must go towards infinity as 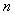 goes to infinity. Thus, goes to infinity. Thus, 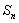 can be less than or equal to can be less than or equal to 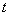 for at most a finite number of values of for at most a finite number of values of 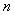 , hence , hence 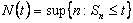 must be finite and one can write must be finite and one can write 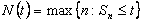
For a better understanding of the concept of renewal theory it is important that we find the distribution of 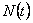 , but before that one must note the important relationship that the number of renewals by time , but before that one must note the important relationship that the number of renewals by time 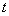 is greater than or equal to is greater than or equal to 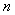 iff the iff the 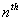 renewal occurs before or at time renewal occurs before or at time 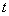 . Hence we need to check the following theorem. . Hence we need to check the following theorem.
Theorem 4.1
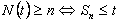
Proof 4.1
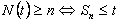
i.e., 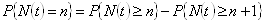
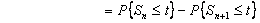
Now 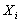 , , 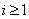 are i.i.d, hence it follows that are i.i.d, hence it follows that 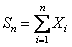 is distributed is distributed 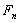 which is the which is the 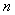 -fold convolution of -fold convolution of 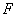 itself which is the distribution of itself which is the distribution of 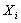 , , 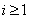 . .
Hence
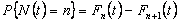 |