Renewal Theory
We know that for a Poisson process, the inter arrival time (a some sort of counting process which counts the inter arrival time in this case) are independent and identically distributed (i.i.d) random variables (r.v.'s) where the underlying distribution is exponential in nature. Consider the counting process has an underlying distribioution and let it be denoted by any arbitrary distribution say, 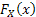 . Then this general counting process is termed as a renewal process. . Then this general counting process is termed as a renewal process.
Before going into details of a renewal process, let us formalize the definition of a counting process. Given any arbitrary distribution, let 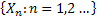 be a sequence of non-negative independent random variables (r.v.'s) (example being the time between the be a sequence of non-negative independent random variables (r.v.'s) (example being the time between the 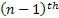 and the and the 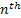 event) with a common distribution, event) with a common distribution, 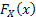 such that such that 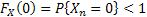 . Let the mean time between successive events be denoted by . Let the mean time between successive events be denoted by 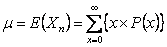 . Now . Now 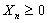 and and 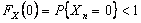 , will ensure that , will ensure that 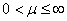 . .
Furthermore let us denote 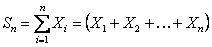 , where , where 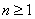 , as the sum of the inter arrival times of , as the sum of the inter arrival times of 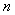 number of such events or better still as the time of the number of such events or better still as the time of the 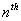 event, with the added condition that event, with the added condition that 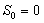 , Figure 4.1. , Figure 4.1.
|