| |
What is convolution
In general functional analysis convolution means that if we have two different functions, 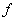 and and 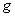 producing a third function, then we denote it by producing a third function, then we denote it by 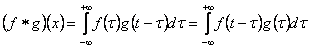 , where the operator denoted by , where the operator denoted by 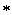 is what is termed as convolution. In general the properties followed by convolution, considering there are two functions, is what is termed as convolution. In general the properties followed by convolution, considering there are two functions, 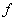 and and 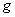 , are: , are:
- Commutative property, i.e.,
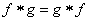
- Associative property, i.e.,
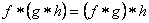
- Distributive property, i.e.,
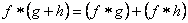
- Associative property with scalar multiplication, i.e.,
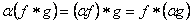
Let us now denote 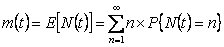 as the renewal function and one of our main focus in renewal theory is to determine the properties of this renewal function. A natural question which arises is how does one understand the importance of this renewal function. as the renewal function and one of our main focus in renewal theory is to determine the properties of this renewal function. A natural question which arises is how does one understand the importance of this renewal function.
Proposition 4.2
Proof of Proposition 4.2
We can write
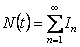 , where , where 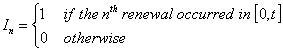
Hence
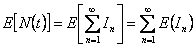
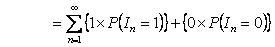
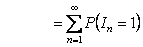
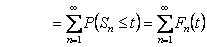
|