Ornstein Uhlenbeck Process
The Weiner process does not provide satisfactory result for the Brownian motion for small values of 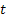 . But for moderate and large values of . But for moderate and large values of 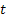 it does provide good results. As alternate model which does good results for small values of it does provide good results. As alternate model which does good results for small values of 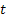 is the Ornstein Uhlenbeck model. The main difference being instead of displacement, is the Ornstein Uhlenbeck model. The main difference being instead of displacement, 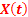 , we consider the velocity, , we consider the velocity, 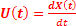 . .
Now the Brownian motion of a particle if expresses using the concept of velocity takes the form of 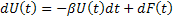 . .
The first term on the right hand side, i.e., 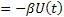 represents the part due to the resistance of the medium in which the particle is, while represents the part due to the resistance of the medium in which the particle is, while 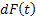 is the random component and is the random component and 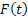 is Weiner process with drift is Weiner process with drift 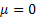 and variance parameter and variance parameter 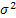 . To make the derivation simply and simplistic we consider . To make the derivation simply and simplistic we consider 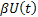 and and 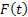 are independent. are independent.
Now for the Markov process 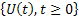 as as 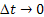 , , 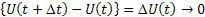 , and we have , and we have
In other words the limit exists hence 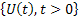 is a diffusion process and it can be proved that its transition p.d.f, i.e., is a diffusion process and it can be proved that its transition p.d.f, i.e., 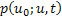 satisfies the forward Kolmorogov equation, with satisfies the forward Kolmorogov equation, with 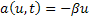 and and 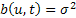 . .
Hence 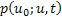 satisfies the differential equation satisfies the differential equation 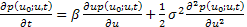 . It can be proves simply by considering the characteristic function that . It can be proves simply by considering the characteristic function that 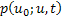 is normal with a mean value of is normal with a mean value of 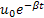 and variance of and variance of 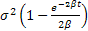 . .
|