| |
Kolmogorov Equations
As usual let us again consider 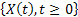 as the Markov process in continuous time and continuous state set up such that the following assumptions are considered to be true: as the Markov process in continuous time and continuous state set up such that the following assumptions are considered to be true:
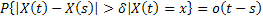 , , 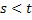
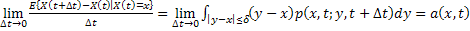 , where , where 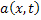 is the drift coefficient. is the drift coefficient.
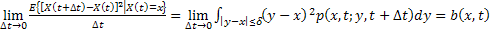 , where , where 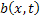 is the diffusion coefficient. is the diffusion coefficient.
Then the corresponding forward Kolmorogov equation and backward Kolmorogov equation are given by:
Note
- In case
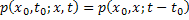 then the Markov process is homogeneous and we have then the Markov process is homogeneous and we have 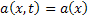 and and 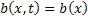 , i.e., both are independent of time , i.e., both are independent of time 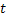 . .
- If the Markov process is additive, then
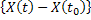 depends only on depends only on 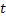 and and 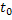 and not on and not on 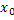 , hence , hence 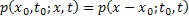 and we have and we have 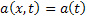 and and 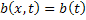 , i.e., both are independent of time , i.e., both are independent of time 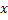 . .
|