Note

• Thus the process  is a Gaussian process with mean  and variance .
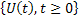
• Thus the process  is a Markov process but it does not possess independent increment like the Weiner process.
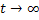
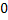
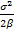
• As , the mean value is  and variance is . This implies the distribution of velocity is in statistical equilibrium.
• The Ornstein–Uhlenbeck process can be interpreted as a scaling limit of a discrete process, in the same way that Brownian motion is a scaling limit of random walks.