Markov Process with discrete state space in continuous time
Till now in all our analysis we considered time component to be discrete and as such transitions occurred at 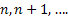 intervals. In case the time component is continuous we need to consider transitions which occur at small time intervals e.g., intervals. In case the time component is continuous we need to consider transitions which occur at small time intervals e.g., 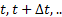 and in the limiting case and in the limiting case 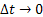 . .
As per our earlier convention let us assume 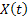 to be a continuous parameter Markov process with state space to be a continuous parameter Markov process with state space 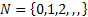 . In case . In case 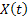 is time homogeneous then we know the transition probability from state is time homogeneous then we know the transition probability from state 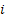 to to 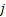 depends only on the state and time interval and not on the initial time when it was at state depends only on the state and time interval and not on the initial time when it was at state 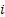 . .
Thus we have the following set of equations which are true for this case.
As the property of time homogeneous holds hence we also have
Furthermore the following facts are also true:
 for each for each 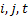 |
(3.4) |
|
(3.5) |
|