| |
Example 3.2
In a branching process the number of off springs per individual has a binomial distribution with parameters 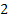 and and 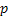 . Starting with a single individual calculate (i) the extinction probability, (ii) the probability that the population becomes extinct for the first time in the third generation. Suppose that instead of starting with a single individual the initial population size, . Starting with a single individual calculate (i) the extinction probability, (ii) the probability that the population becomes extinct for the first time in the third generation. Suppose that instead of starting with a single individual the initial population size, 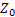 is a random variable that is Poisson distributed with mean, is a random variable that is Poisson distributed with mean, 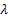 . One can easily show that in this case the extinction probability is given for . One can easily show that in this case the extinction probability is given for 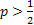 by by 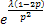 . .
Example 3.3
Consider a branching process in which the number of offspring per individual has a Poisson distribution with mean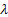 , , 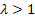 . Let . Let 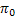 denote the probability that, starting with a single individual the population eventually becomes extinct. Also let , denote the probability that, starting with a single individual the population eventually becomes extinct. Also let , 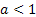 be such that be such that 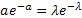 . We can prove that (i) . We can prove that (i) 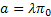 , (ii) conditional on eventual extinction, the branching process follows the same probability law as the branching process in which the number of offspring per individual is Poisson with mean , (ii) conditional on eventual extinction, the branching process follows the same probability law as the branching process in which the number of offspring per individual is Poisson with mean 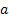 . . |