Waiting time for a change of state
Suppose 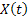 is a homogeneous Markov process and that at time, is a homogeneous Markov process and that at time, 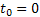 the state of the process the state of the process 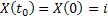 is know to us. Consider the change of the state from is know to us. Consider the change of the state from 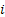 to to 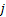 in some arbitrary time in some arbitrary time 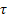 , thus we have , thus we have 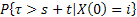 . .
Markov Process with continuous state space in continuous time
In this part we will consider that both state and space changes are continuous in nature. A well known example of this type of stochastic process is the Browian motion. The process derives it name from that of the British botanist by the name of Robert Brown who noticed the random and erratic behavious of pollen grains. Other pioneering work related to this area was done by Einstein and Weiner. Due to its similarities with the concept of diffusion, Brownian motion is also called a diffusion process.
At this stage of our discussion it is imperative to mention that we consider the one dimension Brownian motion only.
|