| |
We already know that if 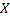 is the random variable (r.v), such that is the random variable (r.v), such that 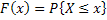 , , 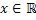 , then , then 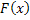 is the distribution function of the random variable (r.v) is the distribution function of the random variable (r.v) 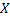 . Consider a finite collection of random variables (r.v's) in . Consider a finite collection of random variables (r.v's) in 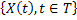 , where , where 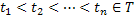 . Then the joint distribution of . Then the joint distribution of 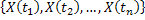 is given by is given by 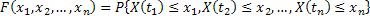 . In case . In case 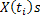 are independent, we have are independent, we have
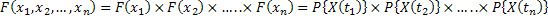 . .
In case they are independent and identically distributed, then the following is true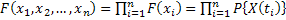 . For example . For example 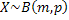 and and 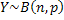 are are
independent but not identical, while 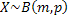 and and 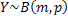 are independent and identical, i.e., i.i.d. are independent and identical, i.e., i.i.d.
|