| |
Example 1.3
Consider the next example of tossing an unbiased coin, where the outcomes are either, a head, 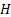 , or tail, , or tail, 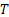 . The associated sample space for this example is . The associated sample space for this example is 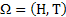 , while , while 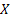 the random variable (r.v) is denoted as the random variable (r.v) is denoted as 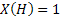 and and 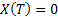 . There is nothing sacrosanct of the fact that . There is nothing sacrosanct of the fact that 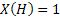 or or 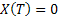 .Pictorially the mapping, which denotes the probability function, is denoted as shown in Figure 1.1. .Pictorially the mapping, which denotes the probability function, is denoted as shown in Figure 1.1.
|
Figure 1.1: Pictorial representation of probability function mapping for the one dimension case |
For the case when we toss two unbiased coins, 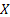 denotes the number of heads/tails appearing. So if we use the same nomenclature for the random variable (r.v), then denotes the number of heads/tails appearing. So if we use the same nomenclature for the random variable (r.v), then 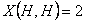 , , 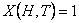 , , 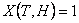 and and 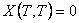 and this simple concept may be illustrated as shown in Figure 1.2. and this simple concept may be illustrated as shown in Figure 1.2.
|
Figure 1.1: Pictorial representation of probability function mapping for the two dimension case |
Hence this concept may be extended to the case of 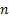 dimensions also, which we omit for the reader to read and clear their concepts from a good book in probability and measure theory. dimensions also, which we omit for the reader to read and clear their concepts from a good book in probability and measure theory. |