| |
Definition of Stochastic Process
Defintion 1
As already mentioned a stochastic process is a function of two parameters which are from the sample space and the parameter space respectively, i.e., 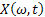 , where , where 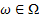 and and 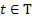 , such that the general nomenclature of denoting a stochastic process is , such that the general nomenclature of denoting a stochastic process is 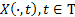 . When the realized value is observed or achieved then we say that the realization of the stochastic process has been observed and it is denoted by . When the realized value is observed or achieved then we say that the realization of the stochastic process has been observed and it is denoted by 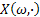 . .
Defintion 2
A Stochastic process is a family of random (r.v.) and they are usually indexed/identifies by say 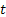 , i.e., its representation is , i.e., its representation is 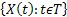 . Here one should remember that . Here one should remember that 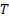 is some index set in a way such that all the elements of is some index set in a way such that all the elements of 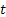 are elements of are elements of 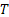 . A realization (or a sample function) of a stochastic process . A realization (or a sample function) of a stochastic process 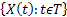 is an assignment to each is an assignment to each 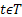 of a possible value of of a possible value of 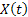 . Here . Here 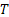 could be finite, countable or uncountable finite. Let us illustrate this with a simple example. could be finite, countable or uncountable finite. Let us illustrate this with a simple example.
|