| |
Basic Probability space, sample space concepts and order of a Stochastic Process
We all know that for a given 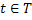 , , 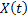 is an random variable (r.v) on some probability space, denoted by is an random variable (r.v) on some probability space, denoted by 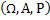 , where , where 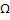 is the sample space, is the sample space, 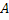 is the is the 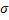 field of subsets of field of subsets of 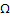 which generates the events, and which generates the events, and 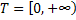 the probability defined on the probability defined on 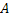 . Thus one can view a stochastic process, . Thus one can view a stochastic process, 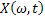 as a family of random variables (r.v's), as a family of random variables (r.v's), 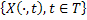 on on 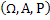 . Hence every fixed value of argument . Hence every fixed value of argument 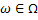 , i.e., every sample point, , i.e., every sample point, 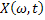 depends only on depends only on 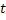 and is simply a function of one real argument, so that for each fixed value of, and is simply a function of one real argument, so that for each fixed value of, 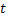 , , 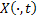 is a real valued function defined on is a real valued function defined on 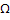 . Furthermore for a fixed . Furthermore for a fixed 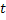 , , 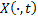 is a random variable (r.v) on is a random variable (r.v) on 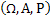 and is a function on and is a function on 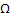 . On the other hand for fixed, . On the other hand for fixed, 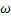 , , 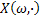 is a function of is a function of 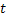 , which represents a possible observation of the stochastic process, and this function , which represents a possible observation of the stochastic process, and this function 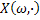 is said to be a realization or a sample function of the process. When several quantities, is said to be a realization or a sample function of the process. When several quantities, 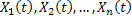 are required for the complete description of the state of the system at a fixed parameter point are required for the complete description of the state of the system at a fixed parameter point 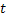 , a generalization can be made accordingly. , a generalization can be made accordingly.
For simplicity we will restrict ourselves to a single quantity 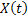 and and 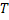 to be one dimension. Thus for a given value of time parameter, to be one dimension. Thus for a given value of time parameter, 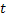 , of the stochastic process, , of the stochastic process, 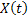 , it is a simple random variable (r.v) and its probability distribution can be obtained as for any other random variable (r.v). But when , it is a simple random variable (r.v) and its probability distribution can be obtained as for any other random variable (r.v). But when 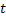 varies in a space varies in a space 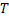 , the information about the process , the information about the process 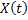 is not provided by a simple distribution for a given is not provided by a simple distribution for a given 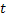 , but one needs the joint distribution of the basic random variables (r.v's) of the family , but one needs the joint distribution of the basic random variables (r.v's) of the family 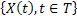 to get the complete information about the process. Obtaining such a joint distribution is impossible if the membership of the family is infinite in number. It then seems reasonable to assume that the behavior of the process can be obtained by studying it at discrete sets of points and accordingly a joint distribution function defined at these points seems reasonable. to get the complete information about the process. Obtaining such a joint distribution is impossible if the membership of the family is infinite in number. It then seems reasonable to assume that the behavior of the process can be obtained by studying it at discrete sets of points and accordingly a joint distribution function defined at these points seems reasonable.
So if 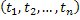 with with 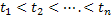 be such a discrete sets of points within be such a discrete sets of points within 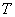 , then the joint distribution of the process , then the joint distribution of the process 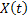 at these points can be defined as at these points can be defined as 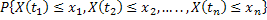 , and this distribution has the simplest form when the random variables (r.v's) are independent. , and this distribution has the simplest form when the random variables (r.v's) are independent.
The study of stochastic process does reduce to the study of simple random variable (r.v). However, in most practical cases, we are faced with the problem of assuming some sort of dependence among the random variables (r.v's). We shall restrict to the simplest type of dependence, called the first order dependence or Markov dependence, which may be understood with the example given below.
|