| |
Example 1.1
Consider we thrown an unbiased dice 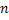 number of times and note the number of times different faces, i.e., number of times and note the number of times different faces, i.e., 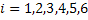 occur, where occur, where 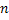 can be can be 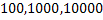 , etc. Now if a theoretical distribution fits this experimental data set, then the expected frequencies/relative frequencies/probability and observed expected frequencies/relative frequencies/probability are compared. In case the fit is good we use the properties of the theoretical distribution to explain the characteristics of the experimental data. Remember in this example we have a static process. Let us illustrate this example in more details, i.e., we have , etc. Now if a theoretical distribution fits this experimental data set, then the expected frequencies/relative frequencies/probability and observed expected frequencies/relative frequencies/probability are compared. In case the fit is good we use the properties of the theoretical distribution to explain the characteristics of the experimental data. Remember in this example we have a static process. Let us illustrate this example in more details, i.e., we have 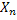 which denotes the random variable (r.v) associated with the which denotes the random variable (r.v) associated with the 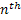 throw of the dice such that: throw of the dice such that:
When we have a sequence of 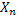 we have a stochastic process which is denoted by we have a stochastic process which is denoted by 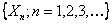 . For the interested reader we would like to mention that this is a Bernoulli process, denoted by . For the interested reader we would like to mention that this is a Bernoulli process, denoted by 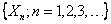 . Stated simply, what we have is a collection or family of random variables (r.v's) which is a stochastic process. But in general to be more specific we have the concept of time also, hence it is a dynamic process, such that a general stochastic process is denoted by . Stated simply, what we have is a collection or family of random variables (r.v's) which is a stochastic process. But in general to be more specific we have the concept of time also, hence it is a dynamic process, such that a general stochastic process is denoted by 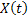 , , 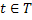 , where , where 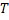 is the parameter space. is the parameter space.
|