Thus a stochastic process is a family of random variables (r.v's) 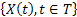 indexed by the parameter indexed by the parameter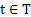 .The values assumed by the stochastic process are called the states and the set of all possible values is called state space. On the other hand the set of possible values of the indexing parameter is called the parameter space, which can be either discrete or continuous. When the indexing parameters are discrete we denote it by .The values assumed by the stochastic process are called the states and the set of all possible values is called state space. On the other hand the set of possible values of the indexing parameter is called the parameter space, which can be either discrete or continuous. When the indexing parameters are discrete we denote it by 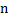 and the stochastic process as and the stochastic process as 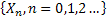 , and this process is what we call a stochastic sequence. In most physical problems time, , and this process is what we call a stochastic sequence. In most physical problems time, 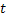 , is the natural index parameter. Other kinds of parameters such as space may also arise, e.g., number of defects on a sheet of metal which can be considered as a stochastic process with the area as the index parameter. But since time is the parameter used in majority of problems, we will use the expression time parameter in a generic sense. , is the natural index parameter. Other kinds of parameters such as space may also arise, e.g., number of defects on a sheet of metal which can be considered as a stochastic process with the area as the index parameter. But since time is the parameter used in majority of problems, we will use the expression time parameter in a generic sense.
Remember, like the parameter space, the state space may also be either discrete or continuous, hence the stochastic process may be any one of the following four (4) types shown in Table 1.1.
Table 1.1: Different types of Stochastic Processes
SNo. |
Parameter Space |
State Space |
Combination |
Examples |
1 |
Discrete |
Discrete |
{Discrete, Discrete} |
Markov Chain |
2 |
Discrete |
Continuous |
{Discrete, Continuous} |
Markov Process |
3 |
Continuous |
Discrete |
{Continuous, Discrete} |
|
4 |
Continuous |
Continuous |
{Continuous, Continuous} |
Brownian Motion |
Thus the nomenclature for denoting the stochactic processes # 1 and # 2 (Table 1.1) is usually, 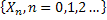 while for # 3 and # 4 (Table 1.1), it is while for # 3 and # 4 (Table 1.1), it is 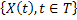 , but in general one uses the latter representation, i.e., , but in general one uses the latter representation, i.e., 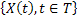 , to represent all the four types of stochastic processes, such that, depending on the domain space of , to represent all the four types of stochastic processes, such that, depending on the domain space of 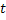 , one can refer whether the process is discrete or continuous. For example we can have , one can refer whether the process is discrete or continuous. For example we can have 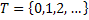 or or 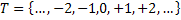 or or 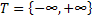 or or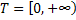 , etc. One should remember that the main emphasis for this lecture series/course would be on Markov chain and Markov process, hence we will study # 1 and # 2 in details. , etc. One should remember that the main emphasis for this lecture series/course would be on Markov chain and Markov process, hence we will study # 1 and # 2 in details.
|