Example 1.12
The concept of transition probability values can be used quite nicely in finance domain, say for example in interest calculation models. Consider the example where we have he interest rate at time period 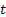 is given by is given by 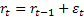 , where , where 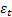 is the error. This is a simple model which is a pure Markov chain example. Next assume is the error. This is a simple model which is a pure Markov chain example. Next assume 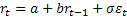 , where , where 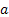 and and 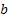 are constants while are constants while 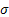 is the volatility. This is a simple AR(1) model. In the second model the volatility can change with respect to time. Furthermore we can assume that this volatility term also follows a Markov chain process. In the simple example we may model the volatility as follows : is the volatility. This is a simple AR(1) model. In the second model the volatility can change with respect to time. Furthermore we can assume that this volatility term also follows a Markov chain process. In the simple example we may model the volatility as follows :
Table 1.2: Scenarios of Volatility
Different researchers have found methods to find the interest rate using different concepts of interest rate calculations. Another method of calculating interest rate can be 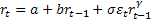 , where , where 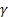 is some index. We can bring more complication in this model by considering is some index. We can bring more complication in this model by considering 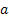 as well as as well as 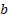 also vary with respect to time. A closer look at the equation will immediately reveal that when also vary with respect to time. A closer look at the equation will immediately reveal that when 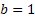 the interest rate will blow up. An important method named the unit root test method has quite a lot of application in interest rate problem, using which we can test for the stationary/non-stationary of the time series, especially interest rate or rate change of stock prices. the interest rate will blow up. An important method named the unit root test method has quite a lot of application in interest rate problem, using which we can test for the stationary/non-stationary of the time series, especially interest rate or rate change of stock prices. |