| |
Further definition of Markov Chain
A stochastic process with discrete state space and discrete parameter space is called a Markov chain. Let us consider a stochastic process with 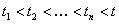 , , 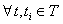 . Now if we have . Now if we have
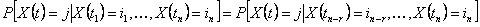 then the stochastic process is called a Markov process of order then the stochastic process is called a Markov process of order 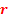 . .
Remember a homogeneous Markov chain of order one is also called a Markov chain, where we denote it simply as 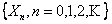
Transition probability and transition matrix
Let us consider the following, i.e., 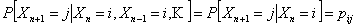 , which is the transition probability of the transition from ith to the jth state in a single step. If the transition property is independent of , which is the transition probability of the transition from ith to the jth state in a single step. If the transition property is independent of 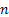 , then it is called the homogeneous Markov chain. , then it is called the homogeneous Markov chain.
One step transition probability
Now 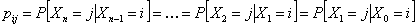 , denotes the probability corresponding to the chance that the stochastic process will move from the ith to the jth state considering that the ith to the jth states can be reached between any two consecutive positions, but generally that may not always be the case. So without any further complication consider , denotes the probability corresponding to the chance that the stochastic process will move from the ith to the jth state considering that the ith to the jth states can be reached between any two consecutive positions, but generally that may not always be the case. So without any further complication consider 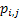 is fixed irrespective of is fixed irrespective of 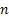 , such that we have , such that we have 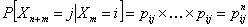 , which is the nth step transition probability which denotes the transition of the particle or body as it goes from state , which is the nth step transition probability which denotes the transition of the particle or body as it goes from state 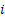 to state to state 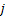 after after 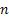 steps. Here steps. Here 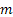 denotes the time instance when the particle is at state denotes the time instance when the particle is at state 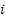 and n is the time units after which it reaches state and n is the time units after which it reaches state 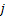 from state from state 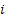 . Hence the total time elaspsed is . Hence the total time elaspsed is 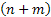 periods. periods.
Now if we bring in the concept of probability mass function, then we one easily add that 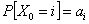 for for for for 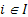 (where I is the state space). Here (where I is the state space). Here 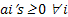 , and , and 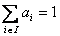 . The second term which is . The second term which is 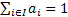 means that the process should definitely start from any one of the positions which is an element of means that the process should definitely start from any one of the positions which is an element of 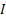 . Utilizing this concept for this simple case we can easily extend this and have the concept of transition probability, which is given by . Utilizing this concept for this simple case we can easily extend this and have the concept of transition probability, which is given by 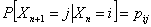 , i, , i, 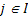 . Here one can deduce that . Here one can deduce that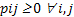 and and 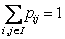 . If we extend the concept of transition probability we have the transition probability matrix given by . If we extend the concept of transition probability we have the transition probability matrix given by 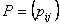 , such that in matrix formulation it is given as , such that in matrix formulation it is given as 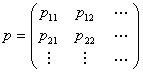 . One should remember that the row sum is 1, i.e., . One should remember that the row sum is 1, i.e., 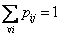 , which is very intuitive. Thus if you are at any ith state then you can move to either 1st or 2nd or any other state, including i th state (i.e., remains at the same position) and no where else. Another important thing to remember about this matrix P, is the fact that it is not an symmetric matrix, as , which is very intuitive. Thus if you are at any ith state then you can move to either 1st or 2nd or any other state, including i th state (i.e., remains at the same position) and no where else. Another important thing to remember about this matrix P, is the fact that it is not an symmetric matrix, as 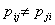 . .
Now 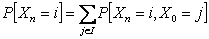
i.e., 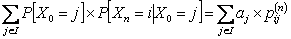 , where , where 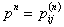 is the n step transition probability matrix and is the n step transition probability matrix and 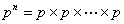 , n times, where, , n times, where, 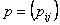 , i.e., , i.e., 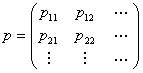 |