Markov Chain
Consider the following where we have (i) State Space : 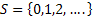 , (ii) Index Set : , (ii) Index Set : 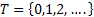 and (iii) event is occurring when and (iii) event is occurring when 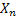 belongs to state belongs to state 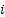 . Figure 1.14 and Figure 1.15 give a diagrammatic view of Markov chain for an ease of understanding of the reader. . Figure 1.14 and Figure 1.15 give a diagrammatic view of Markov chain for an ease of understanding of the reader.
|
Figure 1.14: Illustration of Markov chain |
|
Figure 1.15: Illustration of Markov chain considering initial state i and final state j |
In Figure 1.14 it shows that the movements from state 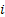 to state to state 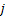 can take place through any direction and they are continuous. But to make our life simple we consider the junps to be in discrete time and the movements are also considered to be discrete, which is depicted in Figure 1.15. can take place through any direction and they are continuous. But to make our life simple we consider the junps to be in discrete time and the movements are also considered to be discrete, which is depicted in Figure 1.15.
The probability of 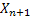 being in state being in state 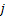 given that given that 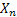 is in state is in state 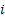 (the concept of one step transition probability) is given by (the concept of one step transition probability) is given by 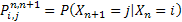 . Using matrix notation it may be represented by the standard matrix representation as shown . Using matrix notation it may be represented by the standard matrix representation as shown 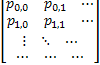 . Few importance properties hold for this transition probability matrix and they are as follows: . Few importance properties hold for this transition probability matrix and they are as follows:
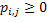 , ,  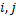 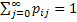 , , 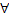 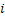 |