| |
Example 1.10
Define 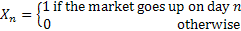
Now the question is, is the market persistent? To answer this we first denote the transition probability matrix 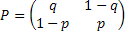 , where the 1st row & 1st column element which is , where the 1st row & 1st column element which is 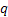 , denotes what is the probability that provided price was at level 0 (this zero is just a notional concept and has nothing to do with its actual value) today, it would continue to be at that price tomorrow also. Similarly the other probabilities signify the other price movements. Now for any particular row (denoted by the suffix , denotes what is the probability that provided price was at level 0 (this zero is just a notional concept and has nothing to do with its actual value) today, it would continue to be at that price tomorrow also. Similarly the other probabilities signify the other price movements. Now for any particular row (denoted by the suffix  ) we have ) we have 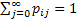 , , 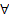 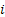 . Hence the corresponding probabilities of 1st row & 2nd column or for that matter 2nd row & 1st column which are . Hence the corresponding probabilities of 1st row & 2nd column or for that matter 2nd row & 1st column which are 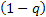 and and 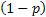 can be easily found given can be easily found given 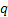 and and 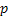 values. This means that values. This means that 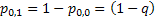 and and 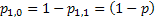 . Even though a repetition we would like to again mention that as . Even though a repetition we would like to again mention that as 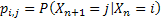 , hence , hence 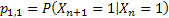 . .
Example 1.11
In line with example 1.9, let us conduct a simple thought experiment, where suppose we are given the state of the prices of a particular stock for 3 consecutive days and assume the price fluctuations are such that they are either 0 or 1. Then the transition probability matrix, P would be denoted as 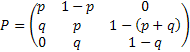 . The question which comes to anyone's mind at this stage is how do we estimate the values of . The question which comes to anyone's mind at this stage is how do we estimate the values of 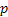 or or 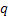 . In case we have the matrix . In case we have the matrix 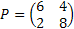 , which is a sample instance of the number of times of movement of stock prices, then the probability values in the long run may be estimated as , which is a sample instance of the number of times of movement of stock prices, then the probability values in the long run may be estimated as 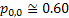 , , 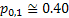 , , 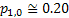 , , 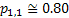 . Another method to calculate the values of . Another method to calculate the values of 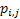 is by using the method of maximum likelihood estimation (MLE) principle, where we look into the likelihood of the data and maximize the value, i.e., is by using the method of maximum likelihood estimation (MLE) principle, where we look into the likelihood of the data and maximize the value, i.e., 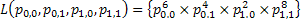 . .
One would immediately recognize that 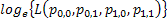 is a monotonic transformed function of is a monotonic transformed function of 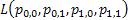 . Moreover based on the following facts that (i) . Moreover based on the following facts that (i) 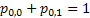 , (ii) , (ii) 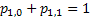 and (iii) and (iii) 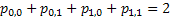 we equate the equations we equate the equations 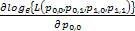 , , 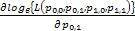 , , 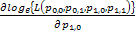 and and 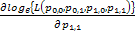 individually to zero and solve them to find individually to zero and solve them to find 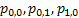 and and 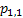 , utilizing their respective estimated values given by , utilizing their respective estimated values given by 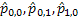 and and 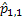 . To find the maximum or minimum value we verify the properties of the Hessian matrix ( . To find the maximum or minimum value we verify the properties of the Hessian matrix (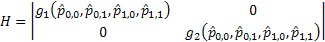 ), where ), where 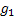 and and 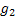 are functions of are functions of 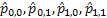 . For the benefit of the reader we would like to mention that . For the benefit of the reader we would like to mention that 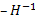 which is the variance/covariance of which is the variance/covariance of 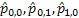 and and 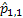 is asymptotically normal. One can also calculate the standard errors of is asymptotically normal. One can also calculate the standard errors of 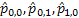 and and 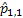 using the MLE approach. using the MLE approach.
|