| |
Example 1.8
Let us now concentrate on an example from civil engineering. Let 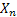 represent the amount of water in a dam at the end of represent the amount of water in a dam at the end of 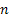 units of time. Suppose during day units of time. Suppose during day 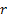 , , 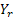 units of water flows into the dam in form of rainfall, supply from rivers, reservoirs, etc., and also assume that units of water flows into the dam in form of rainfall, supply from rivers, reservoirs, etc., and also assume that 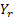 has a particular statistical distribution. As we all know any amount of water cannot be stored in a dam, hence water is discharged from the dam based on the following rule which is, if has a particular statistical distribution. As we all know any amount of water cannot be stored in a dam, hence water is discharged from the dam based on the following rule which is, if 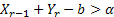 holds true then holds true then 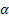 amount of water is dischared, where amount of water is dischared, where 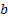 is the capacity of the dam. is the capacity of the dam.
The situation may be represented as follows:
It is easy to note that the dam continues to remain full (i.e., with capacity 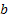 ) until the first negative ) until the first negative 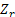 , i.e., the first subsequent day when the amount released exceeds the inflow. On the other hand it will continue to remain empty until the first positive value of , i.e., the first subsequent day when the amount released exceeds the inflow. On the other hand it will continue to remain empty until the first positive value of 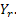 If If 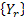 is a sequence of mutually independent and identically distributed random variables that may describe is a sequence of mutually independent and identically distributed random variables that may describe 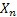 as a simple random walk on the interval as a simple random walk on the interval 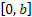 with two reflecting barriers at with two reflecting barriers at 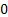 and and 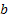 . .
Example 1.9
The next example is from astronomy.Consider that during one revolution around the earth the satellite under goes a change in its energy level. In each successive revolutions the quantum of energy change is assumed to be identical and independently distributed and is denoted by 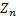 . Thus with an initial energy level of . Thus with an initial energy level of 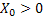 for the satellite, the energy level at time for the satellite, the energy level at time 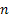 is given by is given by 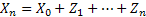 . The satellite escapes the earth¢s gravitational pull if its energy is more than a threshold value of . The satellite escapes the earth¢s gravitational pull if its energy is more than a threshold value of 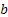 else it falls to the earth if its energy level is less than else it falls to the earth if its energy level is less than 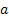 . In that case the situation may be represented by: . In that case the situation may be represented by:
Where 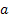 and and 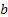 are the absorbing states for this random walk. are the absorbing states for this random walk. |