| |
Example 1.6
Consider we put an item into use and obviously it will fail after some time. When it fails it is replaced by another item of the same type. We may safely assume that 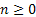 which denotes the lives of the items (they are all similar remember) are independent (a restrictive assumption) and each item fails at the which denotes the lives of the items (they are all similar remember) are independent (a restrictive assumption) and each item fails at the 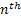 time with a probability denoted by time with a probability denoted by 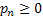 , such that , such that 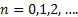 . Also let us consider that the distribution, . Also let us consider that the distribution, 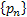 is aperiodic such that is aperiodic such that 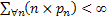 . If . If 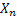 is the age of the item at time is the age of the item at time 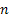 (here is where we bring the time concept as relevant for the Stochastic Process), i.e., the number of periods (including the (here is where we bring the time concept as relevant for the Stochastic Process), i.e., the number of periods (including the 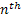 ) it has been in use, then we may assume ) it has been in use, then we may assume 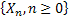 is a random walk (a good example of Markov chain) with the transition probabilities which can be calculated using is a random walk (a good example of Markov chain) with the transition probabilities which can be calculated using 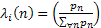 . .
Example 1.7
Consider an insurance company has just started, say at time period 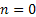 , and the initial fixed capital the company has is , and the initial fixed capital the company has is 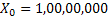 . In due course of time the company receives amounts Y1, Y2,.. in form of premiums and other incomes, while at the same time due to insurance claims and other expenses it has to shelf out amounts denoted by W1, W2,…. . One should remember that these inputs and outputs are happening at same instances of time, which are . In due course of time the company receives amounts Y1, Y2,.. in form of premiums and other incomes, while at the same time due to insurance claims and other expenses it has to shelf out amounts denoted by W1, W2,…. . One should remember that these inputs and outputs are happening at same instances of time, which are 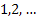 Now the amount of money the insurance company has at any point of time Now the amount of money the insurance company has at any point of time 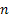 is given by is given by 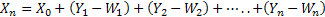 . .
It is obvious that the insurance company goes bankrupt in case 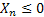 . Thus if we assume that . Thus if we assume that 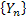 and and 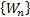 are two separate sequences then are two separate sequences then 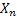 is a random walk starting at is a random walk starting at 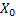 with jumps with jumps 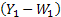 , , 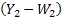 and so on. An interesting thing is the fact that for this random walk we have an absorbing barrier at the origin such that the random walk is denoted by: and so on. An interesting thing is the fact that for this random walk we have an absorbing barrier at the origin such that the random walk is denoted by:
|