| |
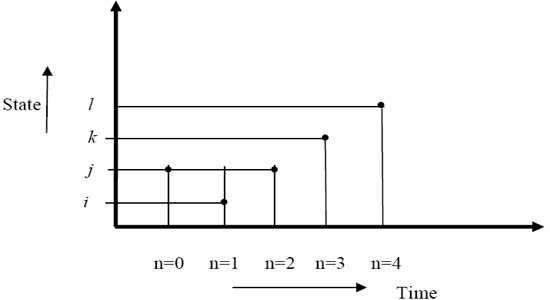 |
Figure 1.13: Arbitrary snapshot of the particle under going random walk |
In case we simplify the above notations then we consider the case where at the starting of the process, i.e., 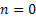 , the particle is at any given point say, , the particle is at any given point say, 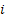 , such that , such that 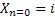 . At time . At time 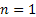 the particle undergoes a jump of quantum Z1 (which is a random variable with a particular distribution). Furthermore at time the particle undergoes a jump of quantum Z1 (which is a random variable with a particular distribution). Furthermore at time 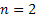 the same particle undergoes another jump Z2 where Z2 is independent of Z1 but has the same distribution as Z1 . Thus the particle undergoes jumps in a manner that after end of the first time period, the same particle undergoes another jump Z2 where Z2 is independent of Z1 but has the same distribution as Z1 . Thus the particle undergoes jumps in a manner that after end of the first time period,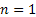 it is at the position it is at the position 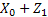 , after the second time period, , after the second time period, 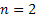 it is at the position it is at the position 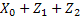 . Thus for . Thus for 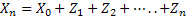 , , 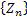 is a sequence of mutually independent and identically distributed random variables. is a sequence of mutually independent and identically distributed random variables.
More generally 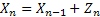 , , 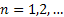 and in case and in case 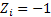 , or , or 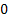 or or 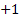 , then what is of interest to , then what is of interest to
us is 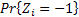 , , 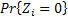 and and 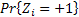 , such that , such that 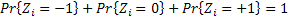 . There may be instances where . There may be instances where 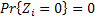 , in which case we should have , in which case we should have 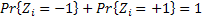 |